O tabuleiro danificado

Um tabuleiro normal, 8 x 8, foi danificado, e 4 posições ficaram esburacadas. A Figura abaixo mostra o tabuleiro. A posição inferior esquerda tem coordenadas (0;0). Os 4 buracos estão marcados em preto, e têm coordenadas (1;3),(2;3),(2;5) e (5;4). Um cavalo de xadrez foi colocado na posição (4;3), marcada como 0 no tabuleiro.

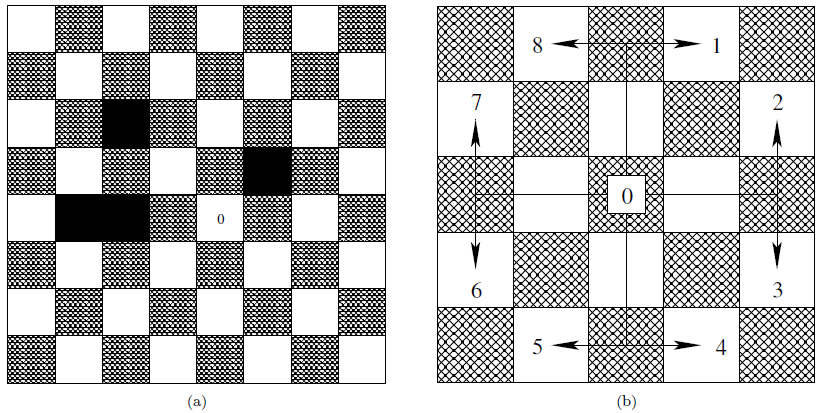
Os 8 movimentos de um cavalo estão numerados de 1 a 8 na Figura 1(b), a partir da posição marcada como 0. Por exemplo, se o cavalo estiver na posição inicial (4;3), o movimento 7 leva o cavalo à posição (2;4), sem cair no buraco (2;3), porque o cavalo salta da posição (4;3) para a posição (2;4). Seu problema é simular um passeio do cavalo, dados os movimentos através dos números de 1 a 8 e determinar quantos movimentos o cavalo faz até ou (i) terminar o passeio ou (ii) cair em um buraco. Por exemplo, na trajetória dada pelos 5 movimentos 1;8;5;3;4, o cavalo passa pelas posições (5;5), (4;7), (3;5) e cai no buraco (5;4), fazendo portanto apenas 4 movimentos. Já no passeio dado pelos 3 movimentos 6;8;1, o cavalo passa pelas posições (2;2), (1;4) e (2;6) e não cai em nenhum buraco: portanto, perfaz todos os 3 movimentos do passeio.

Entrada

A primeira linha da entrada contém N, o número de movimentos do passeio. A segunda linha contém N inteiros M1; M2; ... ;MN, separados por um espaço em branco, correspondentes aos N movimentos do cavalo no passeio. Um movimento pode levar o cavalo a cair em um buraco, mas nunca leva o cavalo a sair do tabuleiro.

Saída

Seu programa deve imprimir uma única linha, contendo um único número inteiro, o número de movimentos do cavalo até terminar o passeio ou o cavalo cair em um buraco.

Restrições

• 1<=N<=100

• 1<=Mi<=8, para I = 1; 2;...;N.

Exemplos

Entrada
5
1 8 5 3 4

Saída
4

Entrada
3
6 8 1

Saída
3